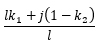サンダーソン補正式とは?
クベルカ・ムンク理論には、光が空気中とコーティング層を行きかう際の部分反射を考慮に入れていません。 サンダーソン補正式はこの部分反射を考慮に入れ、 クベルカ・ムンク理論で必要なコーティングの実反射率を測定反射率から導きます。 (この補正式ができて、初めてクベルカ・ムンク理論が色材の配合計算に実用的になりました。)
<空気中からコート層への光の進行>
光が空気中(屈折率n1)からコート層(屈折率n2)へ進入する際の様子
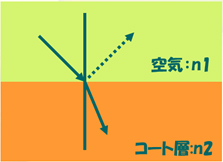
空気中へ表面反射される割合(r)は2つの素材の屈折率で決まります。
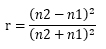
このようにして反射された光は、どこかに放出され二度とこの反射条件に関与することはありません。
<コート層から空気中への光の進行>
光がコート層(屈折率n2)から空気中(屈折率n1)へ進入する際の様子
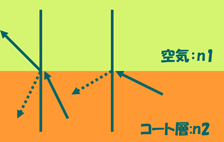
この場合、ある角度より大きくなると、全ての光が反射されて空気中へ進入する光はなくなります。 これらの光の進入の様子はコート層が透過か不透過にかかわらず、屈折率と光の角度および表面の粗さ状態によって決定されます。 空気中/コート層間の光束の関係をモデル化すると下図のようになります。
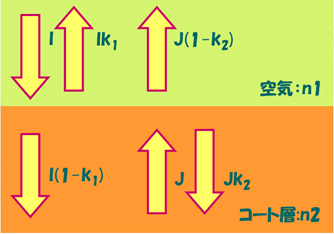
このモデルにおける表面反射率ρは、
ρ(測定反射率)=
しかし、コート層内の実反射率R(クベルカ・ムンクで使用される反射率)は
R(実反射率)= 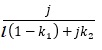
インキと空気の場合、k1、k2の値は、おおむね
k1:0.040
k2:0.600
となります。
(実際は、波長ごとにk1、k2の値は変化します。)
k2の値がk1と比べて大きいのは、インキ内部からの反射は拡散反射になるため、
40°以上の角度の光が全て再度インキ膜内に戻り,この光が再反射され表面へと再度向かいます。
ちなみに、積分球で正反射込み(SPIN)測定を使用する場合、空気中からコート層へ入る際の表面反射は測定値に反映されるため、K1の値は0となります。
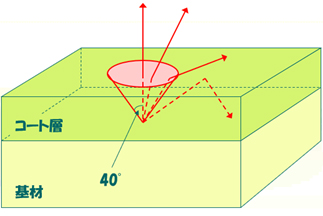
コート層の屈折率=1.5 の場合、法線方向から40°の円錐内の光のみが表面から放出される。
ρ(測定反射率)から 
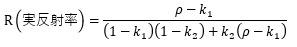
となります。
測定反射率と実反射率の関係は、インク面の場合おおむね以下のようになります。
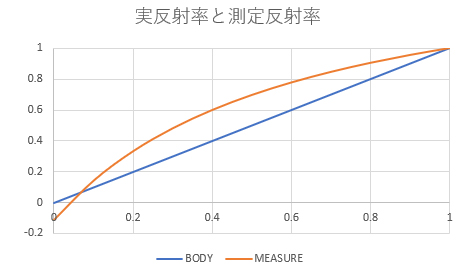
実際の調色ソフトウエアでの運用に関しては、クロスミックス(実際に配合に知れた展色物)を測定して 補正キャリブレーションを設定することで対応することになります。